When selecting a motion system, many users are interested in knowing the maximum acceleration and velocity values of a particular system. It is not always clear how such values are generated, and the resulting miscommunication between user and manufacturer can have surprising consequences for both stage performance and equipment safety. This document will address two key concepts that impact acceleration and velocity. The first is to explore the two most common motion profiles that are used to generate the maximum acceleration and velocity specs that can be found on datasheets throughout the industry. The second is how mass will impact acceleration (and ultimately velocity). Establishing a common language between user and manufacturer for these important specifications is a vital step towards understanding what is being promised on the datasheet, what can be expected from the system, and how to select an appropriate motion system for peak application efficiency.
Consideration of motion profiles generally begins with either a 2nd order profile, or a 3rd order profile. The difference being whether the profile includes Jerk (the derivative of acceleration) as a factor. Many applications don’t require control over this value, and it is often easier to think of a motion as having a period of constant acceleration, an optional period of constant velocity, and a period of constant deceleration. Such a motion is referred to as having a ’2nd order’ or ’trapezoidal’ profile. The position, velocity, and acceleration graphs of this simple profile are shown in Figure 2.1.
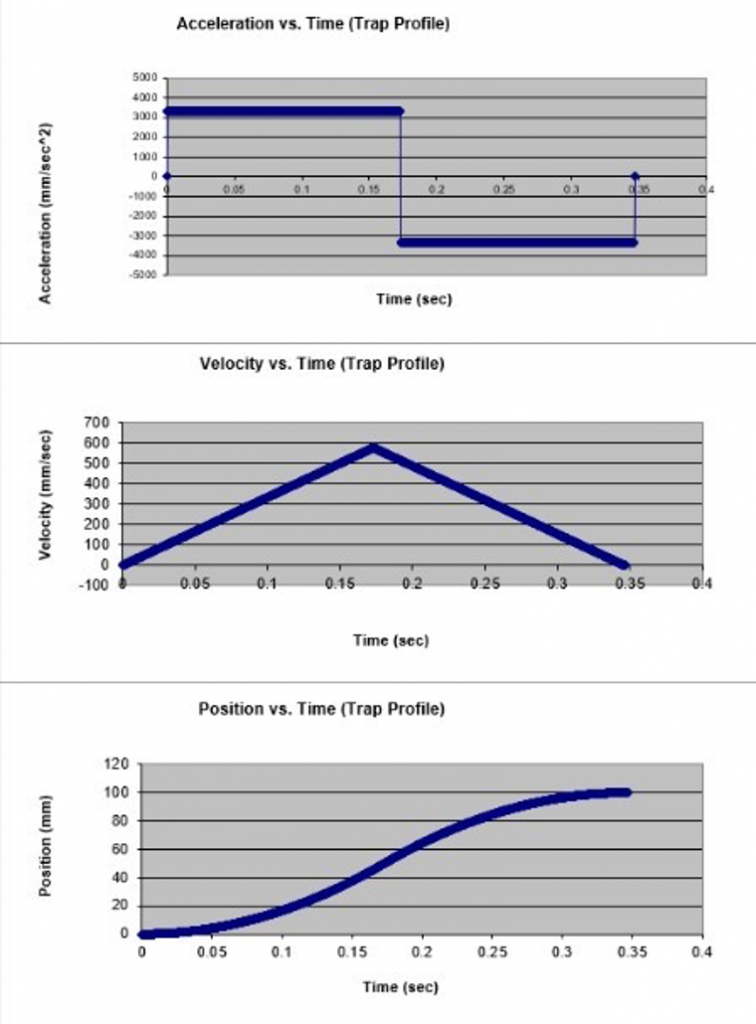
Figure 2.1: A typical 2nd order motion profile.
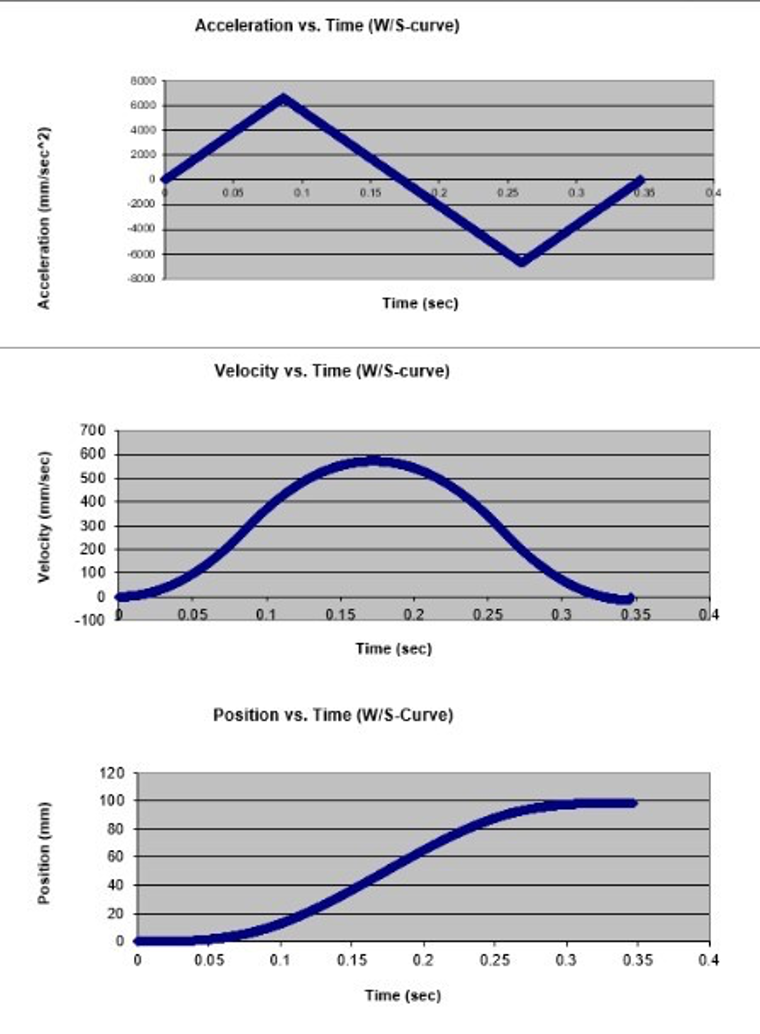
Most precision motion controllers, however, operate one level higher than the trapezoidal profile. Just as it is not possible for a controller to instantaneously change the velocity of a motion system with infinite acceleration, it is equally impossible for the controller to instantaneously change the acceleration of a system with infinite jerk. These controllers will usually take jerk as a motion parameter just like velocity and acceleration when generating a profile. More advanced controllers will also go a step further and provide control over snap (the derivative of jerk), though this is less common. Accounting for jerk results in a ’3rd order’ or ’s-curve’ motion profile. It can be shown that the fastest (and most time efficient) 3rd order profile has no region of constant acceleration and is called a ’100% s-curve’ profile since jerk is non-zero for 100% of the acceleration region. The position, velocity, and acceleration plots of this profile are shown in Figure 2.2. Note that acceleration never reaches a constant value, and instead inflects once it reaches its peak.
Figure 2.2: A typical 3rd order motion profile.
Because of the simplicity of the governing equations and mathematics, it is common for users to ask questions and provide specs from the more direct 2nd order profile standpoint, whereas manufacturers who are familiar with controls will usually provide specs from a 3rd order standpoint. While these two perspectives are closely related and synonymous in many ways, there are discrepancies that can have tangible consequences at the application level.
Relating 2nd and 3rd order profiles is a frequent point of miscommunication between prospective end-users and system manufacturers. It is often in the user’s best interest to specify a motion system that can perform at a level that maximizes the efficiency of a process. As a simple example, a customer may have a sensor with a maximum acceleration spec of 5 m/s2 that they would like to move 100mm as quickly as possible for maximum efficiency. They put a conservative safety factor of 1.5 onto their acceleration spec, bringing it to 3.33 m/s2 and then use a 2nd order calculation to determine their desired motion time of 350ms. The plots of this motion profile are shown in Figure 2.1.
Once the stage is connected to the controller, they will find that their calculated movement is taking significantly longer than they expected. Since the controller generates a 3rd order profile, the system spends the majority of time accelerating more slowly than the nominal value. As a rule of thumb, to match the movement time of a 2nd order profile with constant acceleration, a 3rd order profile will need to momentarily achieve double the 2nd order acceleration. Figure 3.1 shows acceleration plots for both trapezoidal and s-curve profiles taking place over the same distance in the same amount of time. Note that the peak acceleration of the s-curve profile needs to momentarily reach around double the trapezoidal acceleration.
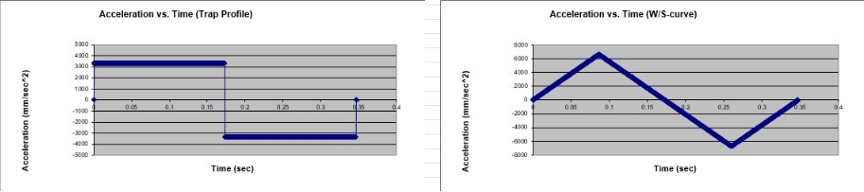
Figure 3.1: Typical 2nd and 3rd order motion profiles.
This means that for the user to perform their motion in the desired amount of time, the peak acceleration of their 3rd order profile will need to be about double their 2nd order acceleration (6.66m/s2). Hence, they cannot perform the desired motion without breaking their sensor’s spec, even with a 1.5 factor of safety!
In this example, the user will be dissatisfied with the slower move times and reduced efficiency. In more extreme cases, this same miscommunication can result in overheating, damaged equipment, and potential for personal injury. This is especially true when the controls are not provided by the manufacturer, and they cannot put safe limits on drive outputs. In these cases, it is critical that users and integrators have a firm grasp on datasheet specifications for maximum acceleration and velocity so they know what movements are safe to command.
When communicating with a stage manufacturer, it is difficult to know for certain that everyone is speaking the same language with regards to motion performance. Asking clear questions including motion profile assumptions is the easiest way to ensure that nobody is making unwarranted assumptions. An example of a common, but unclear, question might be, ”can this system perform a 100mm movement with 3m/s2 acceleration, and a 10% duty cycle?” This question includes a lot of important details, but implicitly calls for a constant acceleration. If the manufacturer knows their stage can only reach a peak of 5m/s2, they have to make some risky assumptions about what question was really being asked. If they assume 3m/s2 is a 2nd order value, they might realize that the time-equivalent 3rd order profile requires 6m/s2, and say ”no.” If they don’t make this assumption they might be overpromising the performance of the system. At best, they might reach out for clarification and increase the time needed for the user to make an informed decision.
Asking the right question takes experience, but there are some tricks that can help.
Specify a Profile – This is the hardest option, but guarantees that everyone is on the same page. ”Can the system move 100mm with a 3m/s2 trapezoidal acceleration profile?
Keep it Time-Dependent – If the application does not require a specific velocity or acceleration, giving the movement as a distance and time will completely avoid the issue of motion profile generation. ”Can the system move 100mm in 0.2 seconds?”
Keep it Open-Ended – This allows the manufacturer to fully consider system capabilities, and report what values can be expected from the system. It is then their responsibility to make it clear which profiles are being considered. ”What is the maximum acceleration the system is capable of over
100mm, at 10% duty cycle?”
When selecting a motion system, maximum motion parameters, such as “Maximum Acceleration” and “Maximum Velocity” are common user questions and on the surface, might be easily answered with a quick check of datasheet specifications. Datasheet specifications, however, may not be telling the full story, as shown in the last section. It is important to read carefully to see how a stage manufacturer qualifies these specifications to get an understanding of how they are calculating them.
Duty Cycle plays a major role in determining allowable acceleration. Duty cycle is a calculated parameter and is based on what percentage of time is spent at the rated acceleration (TON) and what time is spent at no acceleration (TOFF). For a trajectory application, strictly speaking, a 100% Duty Cycle would be an all acceleration (and deceleration), 2nd order move profile. For a 3rd order, 100% S-curve, the calculated duty cycle would be slightly less than 100%, as the Jerk segments would de-rate the calculated value, as acceleration and deceleration “ramp” for a period of time. For the context of this paper, however, we will assume this de-rating is negligible and treat 100% Duty Cycle of the 3rd order the same for the 2nd order.
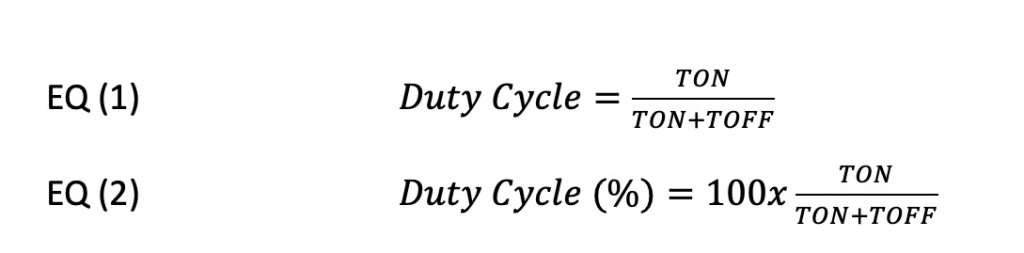
Duty Cycles also plays a role in the calculation of RMS (Root Mean Square) acceleration. The RMS is simply the SQRT(% Duty Cycle/100) * Acceleration. This means for a 50% Duty Cycle, the RMS would 0.707 * Acceleration.
Maximum acceleration can be given in terms of either the 2nd or 3rd order profiles. Higher-order profiles are also possible but will yield similar values to the 3rd order profile. It is most common to give this value in the 3rd order to provide a safe and reliable maximum value for acceleration-sensitive equipment that may be mounted to the stage. Another confounding factor is the difference between ’Peak Acceleration’ and ’Peak Continuous Acceleration.’ Some manufacturers will only list Peak Acceleration, which is generally a more impressive number. This is the acceleration achieved using the motor’s peak current draw for a single, very quick movement. However, such an acceleration can only be performed at a very low duty cycle which makes it impractical for many scanning applications. Attempting to operate a system continuously at peak values without proper protections can cause critical damage to the system and attached components.
In general, the ’Peak Acceleration’ value will be about double the ’Peak Continuous Acceleration,’ which is the acceleration achieved during the most aggressive move that can be sustained at 100% duty cycle continuously. If this continuous value isn’t explicitly called out, it’s best to check in with the manufacturer for accurate numbers.
Mass is another factor that directly impacts acceleration. Datasheets may note what mass is assumed with the stated maximum continuous acceleration. The underlying factor regulating acceleration is the power dissipated in the motor(s), which is further set by the current flowing in the motor and resistance, defined in Equation 3.
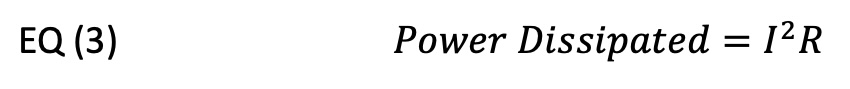
As the moving mass changes, the force required to accelerate changes via Force being equal to mass times acceleration, and consequently, current is changed, governed by Equation 4, where Kf is the “Force Constant” of the motor.

The underlying outcome for peak continuous acceleration is that it is governed by mass, which is variable, application to application, and specified continuous current. The best approach is to work backwards from specified current and Force Constant, getting to force, and then to acceleration through actual mass. Note that these calculations are based an assumed level of heat dissipation within the system. If motor forcers are actively cooled, higher levels of current would be achievable. If, however, motor forcers are isolated thermally, lower current would be required to stay below the maximum allowable stator temperature.
Regarding acceleration designations and mass assumptions, if the manufacturer does not make it clear on their datasheets, it’s worth asking how they calculate their acceleration values to get a complete picture of what performance can be expected of the system.
Maximum velocity is a common question with a complicated answer. Manufacturers will have made numerous assumptions when calculating this value, so many that in fact, the value itself is practically useless. The travel of a system, the necessary period of constant velocity, the back emf of the motor, drive voltage, payload, and many other application-specific factors will impact this value. Assigning a single value to encompass these factors inevitably results in misleading values. If maximum velocity specs are critical, it will always be best to reach out to a manufacturer with your exact application in mind to get an accurate value.
A best-case scenario in terms of datasheet information would be that a “Rated” velocity at “Max Allowable Bus Voltage” is stated. “Rated” is an indicator that the continuous force, governed by continuous current multiplied by the Force Constant, is achievable at the “Rated Velocity”. This puts a stake in the ground from a motor performance point of view, but payload mass, acceleration, and travel have all yet to be considered. It is also common that stated “Bus Voltage” is not the “Maximum Allowable” voltage and further, the application voltage could be something different than either “Bus Voltage” and “Max Allowable”. All of this is to emphasize any difference between actual and stated “Bus Voltage” will impact the maximum velocity available.
Continuing the “Best Case” scenario is to assume the application voltage is equal to the stated bus voltage. This assumption enables a couple key point to progress. First, it links the Continuous Force to the “Rated Speed”. This is important because available force reduces beyond the rated speed. Second, this assumption allows a comparison to be made once we calculate Vmax. Using Equation (5) and the actual payload mass and Continuous Force (Fc), an achievable acceleration can be solved for.
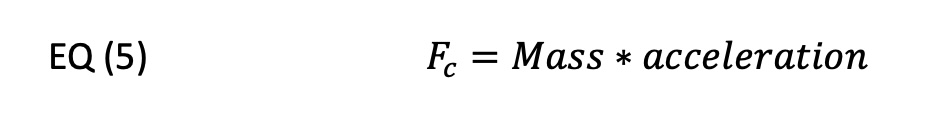
It should be noted that in Equation (5), continuous force is used and not peak force. The simplest form of the 2nd Order Trajectory is for there to be an acceleration and deceleration period, without and constant velocity. In this case, the force needed should be considered as continuous and not peak.
The last calculation step requires the travel distance (D), and knowing that, we can use the 2nd order trajectory equations defined in Equation (6) and (7) to solve for t and then for Vmax

As mentioned above, a comparison of calculated Vmax to stated Vmax is required, as actual Vbus was not used anywhere in the calculation. If the calculated Vmax is less than stated Rated Velocity, the application voltage will support the calculated velocity. If, however, calculated Vmax is larger than stated Rated Velocity, a higher bus voltage will be needed, or a lower acceleration will need to be used, resulting in smaller Vmax and a longer move time. Additionally, if a 3rd order trajectory is implemented, using the available acceleration will drive the actual velocity to be slightly lower, resulting in the actual move time also being slightly longer. 3rd order trajectory equations are available but involve a stated Jerk value and multiple decision steps but would result in a more accurate result.
As discussed, motion profile selection, mass, bus voltage assumptions, and datasheet terminology, all go hand in hand in achieving the desired performance outcomes of acceleration and velocity. Trapezoidal versus S-curve, and “Peak” versus “Peak Continuous” Acceleration are critical parameters where alignment of terminology is necessary. Actual mass and actual Bus Voltage, each play major roles in final performance capability. Open communication is the best method for ensuring success as datasheets and terminology vary from supplier to supplier as well as individual to individual.
Get in touch with ALIO: Expert solutions for your precision motion control needs